ЕГЭ
КАРТОЧКИ
ТЕСТЫ
ОБРАЧАТ
Перпендикулярные прямые
Если вы внимательно изучали предыдущий материал, то можете вспомнить вопрос с подвохом: может ли сумма двух углов составлять $180^\circ$? Мы кратко поясняли, что это действительно возможно, однако лишь в том случае, когда рассматриваются перпендикулярные прямые.
На этом уроке вы узнаете, какие прямые считаются перпендикулярными, что представляет собой перпендикуляр, проведенный из точки к прямой. Мы также рассмотрим взаимосвязь между параллельными и перпендикулярными прямыми и узнаем, почему существует только один перпендикуляр, проведенный из точки.
Перпендикулярные прямые — частный случай
Для начала рассмотрим две произвольные пересекающиеся прямые $a$ и $b$, образующие угол $\alpha$. Как известно, при пересечении двух прямых образуются четыре угла, которые могут быть объединены в смежные или вертикальные пары. Следовательно, любой угол на данном чертеже будет либо смежным, либо вертикальным по отношению к углу $\angle \alpha$.
Если при пересечении прямых один из углов является прямым, то и все остальные углы также будут прямыми. В этом случае рассматриваемые прямые называются перпендикулярными прямыми. Таким образом, перпендикулярные прямые представляют собой частный случай пересекающихся прямых.
Определение перпендикулярных прямых
Перпендикулярные прямые — это прямые, которые пересекаются под углом $90^\circ$.
Для доказательства нам нужно вспомнить свойства смежных и вертикальных углов. Обозначим оставшиеся углы буквами $\beta$, $\gamma$ и $\delta$. Также учтем, что $\angle \alpha = 90^\circ$.
Доказательство
Скрыть
- Угол $\beta$ смежен с углом $\alpha$. Сумма смежных углов равна $180^\circ$, следовательно, $\beta = 180^\circ — 90^\circ = 90^\circ$.
- Так как вертикальные углы равны, угол $\beta$ равен углу $\delta$, а значит, $\delta = 90^\circ$. Аналогично, углы $\alpha$ и $\gamma$ также равны $90^\circ$.
Таким образом:
$\alpha = 90^\circ$, $\beta = 90^\circ$, $\gamma = 90^\circ$, $\delta = 90^\circ$.
Отсюда следует, что перпендикулярные прямые при пересечении образуют только прямые углы, что и требовалось доказать.
Перпендикуляр, проведенный из точки к прямой
Произвольные точка и прямая на плоскости
Перпендикуляр, проведенный из точки к прямой
Рассмотрим произвольную точку $A$ и прямую $a$ на плоскости. Отрезок $AB$, проведенный из точки $A$ к прямой $a$, называется перпендикуляром, если он образует с данной прямой угол $90^\circ$. Точка пересечения прямой $a$ и отрезка $AB$ называется основанием перпендикуляра.
Иными словами, перпендикуляр, проведенный из точки к прямой, — это отрезок прямой, перпендикулярной к заданной, один конец которого принадлежит точке пересечения с ней.
Перпендикуляр, проведенный из точки к прямой: нотация
В геометрической нотации перпендикулярность обозначается символом «$\perp$». Например, если прямые $a$ и $b$ перпендикулярны, то запись имеет вид: $a \perp b$. Если речь идет об отрезке $AB$, проведенном перпендикулярно к прямой $a$, то пишут: $AB \perp a$.
Единственность перпендикуляра
В геометрии справедливо следующее утверждение: через любую точку прямой можно провести только один перпендикуляр к ней. Это свойство называется единственностью перпендикуляра.
Теорема о единственности перпендикуляра
Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Доказательство
Скрыть
Воспользуемся доказательством от противного. Предположим, что данное утверждение неверно, и через одну точку прямой проходят два различных перпендикуляра — $b$ и $c$.
По определению, угол между прямыми $a$ и $b$ равен $90^\circ$, и аналогично угол между прямыми $a$ и $c$ также равен $90^\circ$. Однако от прямой можно отложить только один угол данной градусной меры, следовательно, возникло противоречие.
Таким образом, теорема доказана, и перпендикуляр через одну точку может быть проведен лишь один.
Интерактив
В интерактиве показано, как из точки можно построить единственный перпендикуляр к прямой. Перемещайте точку и нажимайте кнопку, чтобы увидеть построение. Этот опыт поможет убедиться в важном свойстве: перпендикуляр к прямой из точки всегда существует, и он только один.
Это интересно: перпендикулярные прямые и отвес
Рассмотрим бытовой пример. Допустим, вы решили повесить полку на стену. После установки возникает сомнение — висит ли она ровно? Чтобы убедиться в этом, достаточно воспользоваться простейшим инструментом, известным с древности, — отвесом.
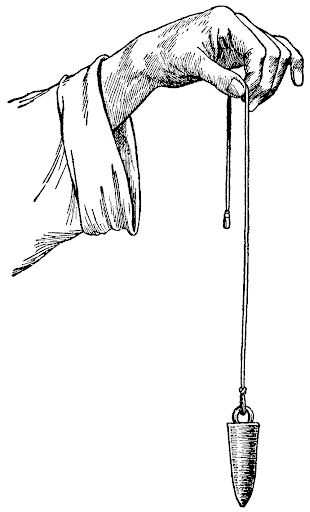
Отвес представляет собой груз, прикрепленный к гибкой нити. Благодаря своей форме и массе он позволяет нити растянуться строго вертикально, показывая направление силы тяжести. Если прикрепить отвес к потолку, можно определить, находится ли полка перпендикулярно стене, то есть образует ли с ней угол $90^\circ$.
Интересный факт: древние римляне называли отвес словом 'perpendiculum', происходящим от глагола 'perpendō', что означает «я точно измеряю». Отсюда и происходит современное слово «перпендикуляр» и связанные с ним понятия.
Параллельные и перпендикулярные прямые
Если ваша полка висит идеально ровно относительно потолка, то прямые, соответствующие их положению, будут параллельными.
Параллельные прямые — это прямые, лежащие в одной плоскости и не имеющие общих точек пересечения.
Теперь рассмотрим случай, когда две прямые $a$ и $b$ параллельны, а третья прямая $c$ перпендикулярна к $a$. Если $c \perp a$, то она будет перпендикулярна и к $b$, при условии, что $a \parallel b$. Это утверждение можно доказать методом доказательства от противного.
Обратное также верно: если две или более прямые перпендикулярны к одной и той же прямой, то они параллельны между собой.
Часто задаваемые вопросы
Две прямые называются перпендикулярными прямыми, если при их пересечении образуется угол в $90^\circ$. На чертежах такой угол обычно обозначают небольшим квадратиком в вершине угла. В алгебраической форме перпендикулярность записывается как $a \perp b$, где $a$ и $b$ — пересекающиеся прямые.
Нет, через одну точку прямой можно провести только один перпендикуляр. Это утверждение выражает теорему о единственности перпендикуляра. Если бы из одной точки можно было провести два различных перпендикуляра, то к одной прямой существовало бы два различных угла по $90^\circ$, что невозможно.
Если прямая $c$ перпендикулярна к прямой $a$, а прямая $a$ параллельна прямой $b$, то прямая $c$ будет перпендикулярна и к $b$. Аналогично, если две прямые перпендикулярны к одной и той же прямой, они являются параллельными. Таким образом, перпендикулярность и параллельность связаны между собой через общие геометрические свойства.
5
5
1
5
Получите полный доступ ко всем материалам и занимайтесь в удобном темпе — без ограничений.
- Более 700 000 учеников и 50 000 учителей по всей России.
- Повышение среднего балла по предмету до 20 % после месяца занятий.
- Всплеск интереса к учебе и более глубокое понимание предметов.
Создайте бесплатный аккаунт — и откройте больше возможностей:
- Отслеживайте прогресс освоения тем
- Получайте персональные подборки полезных уроков и заданий
- Проводите работу над ошибками после занятий
Оценить урок
Что можно улучшить?
Войдите, чтобы оценивать уроки
Что нужно исправить?
Отзыв отправлен. Спасибо, что помогаете нам стать лучше!
Хотите оставить комментарий?
Войти