Измерение углов

На прошлом уроке выяснилось, что единицей измерения углов и дуг является градус, равный $\frac{1}{360}$ окружности. Измерение углов, следовательно, представляет из себя «процесс нахождения», сколько частей окружности ($\frac{x}{360}$) заключено между сторонами угла.

Это отвечает на большую часть вопросов, что мы задавали ранее, однако не на все. Теперь, когда у нас есть единица измерения, нужно разобраться с правилами, определяющими, что в себя включает геометрия измерения углов.

Измерение углов — основное свойство

Начертим на плоскости угол $\angle{BAC}$ и проведем между его сторонами $AB$ и $AC$ луч $AD$. Допустим, нам известна градусная мера $\angle{DAC}$ и $\angle{BAD}$.

Чему будет равен $\angle{BAC}$?

Мы помним аксиому, задающую, что длина отрезка равняется сумме длин частей, на которые он разбивается любой его точкой. Измерение углов также подчиняется аксиоме «длины», только, конечно, вместо «длины» мы будем говорить «градусной меры»:

$A_8$. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Геометрия измерения углов: $0^\circ$

Включает ли в себя геометрия измерения углов нулевые величины? Оказалось, что аксиома суммы частей применима как к отрезкам, так и к углам. А применима ли к углам аксиома «нулевой фигуры»? В отличие от отрезка, длина которого всегда задается строго больше нуля, о нулевых углах говорить можно.

Учтите, что в некоторых учебниках тем не менее встречается следующая аксиома: «Каждый угол имеет определенную градусную меру, бóльшую нуля». Это не совсем верно, поскольку тригонометрические функции могут принимать аргумент в виде нуля. Даже отрицательные аргументы.

Что это означает — не суть. Главное, что далее в курсе математики измерение углов может иметь дело с условным $\angle{A}=0^\circ$. Чтобы путаницу предупредить, аксиому углов $>0$ мы вводить не будем. А угол, равный нулю, будем представлять как угол, у которого стороны являются совпадающими лучами.  

Измерение углов — основное свойство: задача

Условие. Проведено измерение углов, в результате которого получены следующие градусные меры: $\angle{FDK}=38^\circ$, $\angle{KDM}=26^\circ$, $\angle{MDA}=32^\circ$.

Чему равен $\angle{FDA}$?

{"questions":[{"content":"[[image-4]]Известно, что $\\angle{DAB}=10^\\circ$. Чему равняется градусная мера угла $\\angle{CAD}$, если $\\angle{CAB}=68^\\circ$? [[speech-1]]<br>[[input-23]]","widgets":{"speech-1":{"type":"speech","text":"Аксиома в помощь!"},"image-4":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/09/ex-test.svg","width":"400"},"input-23":{"type":"input","unit":"$^\\circ$","answer":"58"}},"step":1,"hints":["По аксиоме суммы градусных мер углов про $\\angle{CAB}$ можно заключить, что:<br />$$\\angle{CAB}=\\angle{CAD}+\\angle{DAB}$$","Градусные меры углов $\\angle{CAB}$ и $\\angle{DAB}$ известны из условия. Значит, чтобы найти градусную меру $\\angle{CAD}$, нужно найти значение разности градусных мер углов $\\angle{CAB}$ и $\\angle{DAB}$.","Вычисляем: <br />$$\\angle{CAD}=\\angle{CAB}-\\angle{DAB}=68^\\circ-10^\\circ=58^\\circ$$"]}]}

Измерение углов транспортиром

Измерительным инструментом углов является транспортир. Он представляет из себя пластину, выполненную в форме круга или полукруга, основанием которого иногда бывает линейка. Разметка полукругового транспортира состоит из 180 градусов, кругового — из 360. По своей сути транспортир — это конечный результат идеи о делении окружности на 360 ровных частей и нанесении на окружность соответствующей разметки.

Полукруговой транспортир

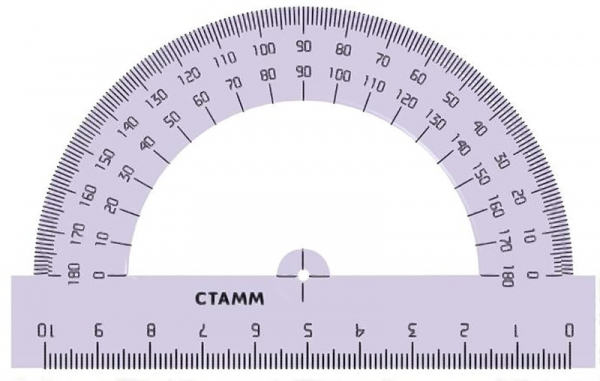
Круговой транспортир

Как пользоваться транспортиром для измерений

Измерение углов в школьном курсе геометрии вполне обходится упрощенной версией транспортира — полукруговой. На самом деле, транспортир используется не только для измерения, но и для построения углов. Вначале мы разберем, как проводить измерение углов транспортиром.

Шаг первый  

Совместите точку отсчета инструмента с вершиной измеряемого угла. Одну из сторон угла расположите параллельно основанию транспорта: эта сторона должна указывать на нулевую отметку.   

Шаг второй

Совместив основание со стороной угла, можно переходить к измерению угла. Вторая сторона угла будет указывать на некоторую отметку градусной шкалы. Если вдруг «поворотная» сторона не доходит до разметки, дорисуйте ее линейкой до необходимой длины.

Шаг третий

Зафиксируйте величину угла. Измерение углов транспортиром не допускает округление градусной меры без необходимости. Если транспортир показывает «$61^\circ$», не стоит округлять значение до «$60^\circ$».

В нашем же случае угол составляет ровно $60^\circ$.

Как начертить угол транспортиром

Выше было продемонстрировано измерение углов с помощью транспортира без вспомогательной линейки. Транспортиры с основанием в виде сантиметровой линейки — тоже полезный инструмент, в особенности для откладывания углов. Давайте посмотрим, как начертить угол транспортиром, откладывая при этом на сторонах угла отрезки определенной длины.

Задача. Отложить $\angle{BAC}=80^\circ$ так, чтобы при этом отрезки $AC$ и $AB$ равнялись $4~см$ и $3~см$ соответственно.

☝️ Откладываем сторону на основании

В первую очередь на риске отсчета отметим точку $A$ — это будет вершина откладываемого угла. Проведем от точки $A$ луч, параллельный основанию транспортира. Первая часть откладывания угла выполнена.  

✌️Откладываем вторую сторону угла

Чтобы начертить угол транспортиром, необходимо отметить еще одну точку на отметке $80^\circ$. Отметим риску $80^\circ$ небольшой вспомогательной точкой. Теперь проведем через эту вспомогательную точку и точку $A$ луч.

Нюанс!

Обратите внимание, что углы принято откладывать против часовой стрелки. Альтернативная разметка ниже основной — по часовой стрелке — предлагается на транспортире, чтобы было удобно проводить измерение углов. Ориентация углов на плоскости разная, и не всегда бывает хорошо иметь под рукой разметку, нанесенную только против часовой стрелки.

Построения линейкой

Руководствуясь условием поставленной задачи, отметим точку $C$ на основании таким образом, чтобы расстояние между точками $A$ и $C$ составляло $4~см$. Применим для этого линейку. Проделаем ту же самую последовательность действий с точкой $B$ с поправкой на $AB=3~см$.

Немного самостоятельной практики!

Возьмите карандаш, транспортир и лист бумаги. Отложите от стороны на основании транспортира два произвольных угла в границе $0^\circ<x<180^\circ$. Поделитесь в комментариях к уроку, какие градусные меры вы выбрали для углов.

Типы углов по градусам

Вероятно, ранее вам приходилось слышать определения для углов наподобие «острый», «тупой» и так далее. Эти определения задают типы углов по градусам. Зачем и кому это нужно? Цель очень даже приземленная: типы углов по градусам позволяют быстро сориентироваться, в каких границах значений располагается градусная мера угла. «Острый», «тупой» и прочее — это слова-маркеры.

Предлагаем с этими маркерами познакомимся поближе, дабы научиться проводить измерение углов на глаз.

Острый угол. Угол, градусная мера которого располагается в границах $0^\circ\leq{x}<90^\circ$. Заметьте, что угол, составляющий $0^\circ$, считается острым. Пример острого угла: $\angle{\alpha}=50^\circ$.

Тупой угол. Угол, градусная мера которого располагается в границах $90^\circ<x<180^\circ$. Пример тупого угла: $\angle{\beta}=130^\circ$.

{"questions":[{"content":"Известно, что $\\angle{A}=89^\\circ$, а $\\angle{B}=91^\\circ$. Какой из данных углов будет относиться к тупым, а какой — к острым? [[matcher-1]]","widgets":{"matcher-1":{"type":"matcher","labels":["$\\angle{A}$","$\\angle{B}$"],"items":["Острый","Тупой"]}}}]}

Развернутый и прямой углы. Заметьте, что выше границы для $90^\circ$ и $180^\circ$ устанавливаются строгими неравенствами. Это важные доли окружности, поэтому для них имеются отдельные названия. Так, угол, равный $90^\circ$ ($\frac{1}{4}$ окружности), называется прямым. Угол в $180^\circ$ ($\frac{1}{2}$ окружности) называется развернутым.

Прямой угол ($90^\circ$)

Развернутый угол ($180^\circ$)

{"questions":[{"content":"[[speech-1]][[choice-5]]","widgets":{"speech-1":{"type":"speech","text":"Допустим, $\\angle{A}=90,1^\\circ$. Можем ли мы пренебречь частью после запятой и заключить, что $\\angle{A}$ — <b><i>прямой</i></b> угол?"},"choice-5":{"type":"choice","options":["Да, $\\angle{A}$ — прямой.","Нет, прямой угол должен быть строго $90^\\circ$."],"explanations":["","Верная мысль. Поскольку $\\angle{A}>90^\\circ$, хоть и всего на десятую долю, он будет считаться тупым."],"answer":[1]}}}]}

Выпуклый угол. Когда градусная мера угла располагается в границах $180^\circ<x<360^\circ$, такой угол называется выпуклым.

Например, выпуклым углом является $\angle{\gamma}=260^\circ$.

Выпуклые углы удобнее измерять круговым транспортиром. Однако если в наличии только полукруговой, можно вначале «отбить» развернутый угол ($180^\circ$), а остальную часть измерить как острый угол. Полученное значение складывается с градусной мерой развернутого угла. На примере угла выше:

$$180^\circ+80^\circ=260^\circ$$

Полный угол. Под полным углом понимается угол, равный полному обороту окружности, то есть составляющий $360^\circ$.

Заметьте, что стороны полных и нулевых углов располагаются на одной прямой.  

{"questions":[{"content":"Известны следующие величины углов: $\\angle{A}=90^\\circ$, $\\angle{B}=310^\\circ$, $\\angle{C}=72^\\circ$, $\\angle{B_1}=180^\\circ$, $\\angle{A_1}=360^\\circ$, $\\angle{A_2}=90,5^\\circ$, $\\angle{D}=180,3^\\circ$, $\\angle{F}=135^\\circ$, $\\angle{\\alpha}=1^\\circ$.<br /><br /><i>Распределите углы согласно подходящим типам по градусам.</i> [[grouper-1]]","widgets":{"grouper-1":{"type":"grouper","labels":["Полный угол","Прямой угол","Тупые углы","Острые углы","Развернутый угол","Выпуклые углы"],"items":[["$\\angle{A_1}$"],["$\\angle{A}$"],["$\\angle{A_2}$","$\\angle{F}$"],["$\\angle{С}$","$\\angle{\\alpha}$"],["$\\angle{B_1}$"],["$\\angle{B}$","$\\angle{D}$"]]}}}]}