Равнобедренный треугольник. Свойства равнобедренного треугольника

Обновленный урок по теме: «Равнобедренный и равносторонний треугольники»

Сегодня мы погрузимся в мир треугольников — одной из самых важных фигур в геометрии. Вы уже знакомы с разными видами треугольников, а сегодня сосредоточимся на особом их представителе — равнобедренном треугольнике: узнаем, что делает его «особенным», разберемся, как отличить его от других фигур и какие элементы в нем играют ключевую роль.

Равнобедренный треугольник не просто красив с точки зрения симметрии — он обладает рядом уникальных свойств, которые помогают решать множество геометрических задач. На уроке мы сформулируем эти свойства, докажем их и научимся применять на практике.

Понятие равнобедренного треугольника

Наиболее знаменательным древнеегипетским архитектурным сооружением является пирамида Хеопса. Найти ее любознательный путешественник может в пригороде Каира — современной столицы Египта. Боковые грани пирамиды — это четыре равнобедренных треугольника.

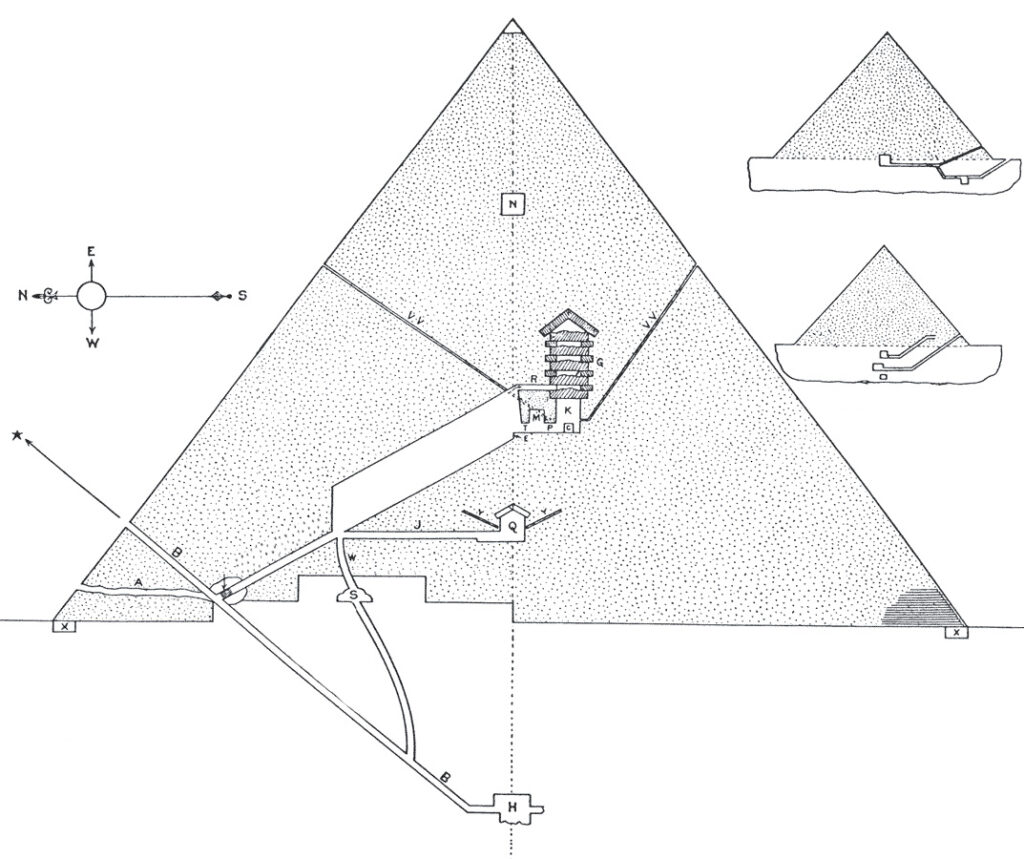
Обратите внимание на схематичное изображение пирамиды Хеопса в поперечном разрезе. В треугольнике, подобном граням пирамид Древнего Египта, боковые стороны являются равными по величине. Это — частный случай геометрии треугольников, который мы с вами сегодня и будем разбирать.

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по величине.

Значит, равнобедренный треугольник имеет равные «бедра» — боковые стороны при основании.

На чертеже такой треугольник изображен и размечен отдельно. Посмотрите: в $\bigtriangleup{ABC}$ имеется основание $AB$ и боковые стороны $BC$ и $CA$, при этом $BC=CA$.

В случае с произвольным треугольником с произвольно заданными сторонами и углами особой роли не играет, как вы разместите его на чертеже. Можно под углом, можно основанием параллельно краю листа.

Равнобедренный треугольник традиционно располагают по принципу грани древнеегипетской пирамиды — основанием к «земле», то есть к низу, не под углом.

Показать решение

Скрыть

{"questions":[{"content":"В равнобедренном треугольнике равны [[fill_choice_big-20]].","widgets":{"fill_choice_big-20":{"type":"fill_choice_big","options":["две стороны","три стороны","три угла"],"answer":0}},"hints":["Треугольник с тремя равными сторонами называется равносторонним и является частным случаем равнобедренного."]}]}

Свойства равнобедренного треугольника

Теорема равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны.

Доказательство

Скрыть

Дан равнобедренный треугольник $\bigtriangleup{ABC}$ с основанием $AB$. По определению $BC=CA$. Проведем в треугольнике биссектрису $CD$ к основанию и рассмотрим треугольники $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$.

Они равны по первому признаку равенства треугольников, то есть по двум сторонам и углу между ними: $BC=CA,$ $\angle{DCA}=\angle{BCD},$ биссектриса $CD$ — общая сторона. Если треугольники равны, то против равных сторон в них будут лежать равные углы. Откуда делаем вывод, что $\angle{CAB}=\angle{ABC}$. Теорема равнобедренного треугольника доказана.

Мы помним, что периметр — сумма всех сторон треугольника. Равнобедренный треугольник имеет равные стороны при основании, так что для случая с таким треугольником формулу периметра можно немного трансформировать: $P=2a+b$, где $a$ — длина боковой стороны, $b$ — длина основания.

{"questions":[{"content":"Известно, что угол при основании равнобедренного треугольника равен $65^{\\circ}$, а сумма углов треугольника составляет $180^{\\circ}$.<br><br>Чему равен угол, противолежащий основанию? [[fill_choice_big-21]]","widgets":{"fill_choice_big-21":{"type":"fill_choice_big","options":["$50^{\\circ}$","$45^{\\circ}$","$35^{\\circ}$","$80^{\\circ}$"],"placeholder":0,"answer":0}},"step":1,"hints":["Вспомним, что углы при основании равнобедренного треугольника равны: $65^{\\circ}+65^{\\circ}=130^{\\circ}$.","Вычтем полученную сумму из $180^{\\circ}$: $180^{\\circ}-130^{\\circ}=50^{\\circ}$."]}],"mix":1}

Медианы, биссектрисы, высоты равнобедренного треугольника

На чертеже равнобедренного треугольника выше внимание привлекает вот что: биссектриса равнобедренного треугольника как будто бы является одновременно и высотой в треугольнике, и медианой.

Одно из главных свойств равнобедренных треугольников заключается в том, что, проводя, к примеру, медиану к основанию, вы получаете в то же самое время высоту и биссектрису равнобедренного треугольника. И это все один отрезок. Сформулируем на основе наших предположений теорему и докажем ее.

Теорема о медиане, биссектрисе и высоте равнобедренного треугольника.
В равнобедренном треугольнике медиана, проведенная к основанию, является и высотой, и биссектрисой.

Доказательство

Скрыть

Дан равнобедренный треугольник $\bigtriangleup{ABC}$. К основанию $AB$ проведена медиана $CD$.

Треугольники $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$ будут равны по первому признаку равенства треугольников: $\angle{CAB}$ и $\angle{ABC}$ равны по теореме об углах равнобедренного треугольника, стороны $BC$ и $CA$ равны по определению равнобедренного треугольника, $AD=DB$ по определению медианы.

Из равенства треугольников следует равенство углов $\angle{ACD}$ и $\angle{BCD}$. Тогда $CD$ — биссектриса. Углы $\angle{ADC}$ и $\angle{BDC}$ равны из доказанного равенства треугольников $\bigtriangleup{ADC}$ и $\bigtriangleup{DBC}$. Эти углы являются смежными.

Раз сумма смежных углов равна $180^{\circ}$ и углы при этом равны, то они оба равняются $90^{\circ}$. Из этого следует, что $CD$ — высота. Теорема доказана.

Если проводите в равнобедренном треугольнике, скажем, медиану к основанию, сразу отмечайте на чертеже свойство высоты и биссектрисы. Это поможет постоянно иметь перед глазами свойства равнобедренного треугольника, что значительно облегчит доказательство утверждения или решение задачи.  

{"questions":[{"content":"Будет ли биссектриса равностороннего треугольника являться и медианой, и высотой, если она проведена к боковой стороне, а не к основанию? [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["Да","Нет"],"answer":[0]}},"step":1,"hints":["Равносторонний треугольник наследует свойства равнобедренного треугольника. Значит, у него каждая сторона может выступать в роли своего рода «основания равнобедренного треугольника».","Следовательно, к какой бы стороне мы ни проводили биссектрису, она будет и медианой, и высотой."]}]}

Практика

задача

На рисунке изображен $\bigtriangleup{ABC}$, где $BC=CA$. Известно, что $\angle{1}=130^{\circ}$. Чему равняется значение угла $\angle{2}$?

Показать решение

Скрыть

задача

В равнобедренном треугольнике $\bigtriangleup{ABC}$ с основанием $AB$ проведена медиана $CD$. Найдите длину медианы $CD$, если периметр треугольника $\bigtriangleup{ABC}$ равен $32~см$, а периметр треугольника $\bigtriangleup{ADC}$ равен $24~см$.

Показать решение

Скрыть

Часто задаваемые вопросы