Координаты точки

Ранее мы научились находить координату точки на прямой линии (или числовой оси). 

Как же найти месторасположение точки не на прямой, а на плоскости? 

В предыдущем уроке вы узнали, что проще находить координаты объекта на плоскости с помощью двух чисел в прямоугольной системе координат.

Представим, например, стол и какую-то точку $А$ на нем. 

В прямоугольной системе координат длину стола можно отмерить по оси $Ox$, а ширину по перпендикулярной ей оси $Оу$, место их пересечения будет точкой отсчета $О$. 

Тогда местоположение нашей точки $А$ можно найти, проведя от нее перпендикулярные прямые к каждой из осей. Эти линии обычно изображаются пунктиром. 

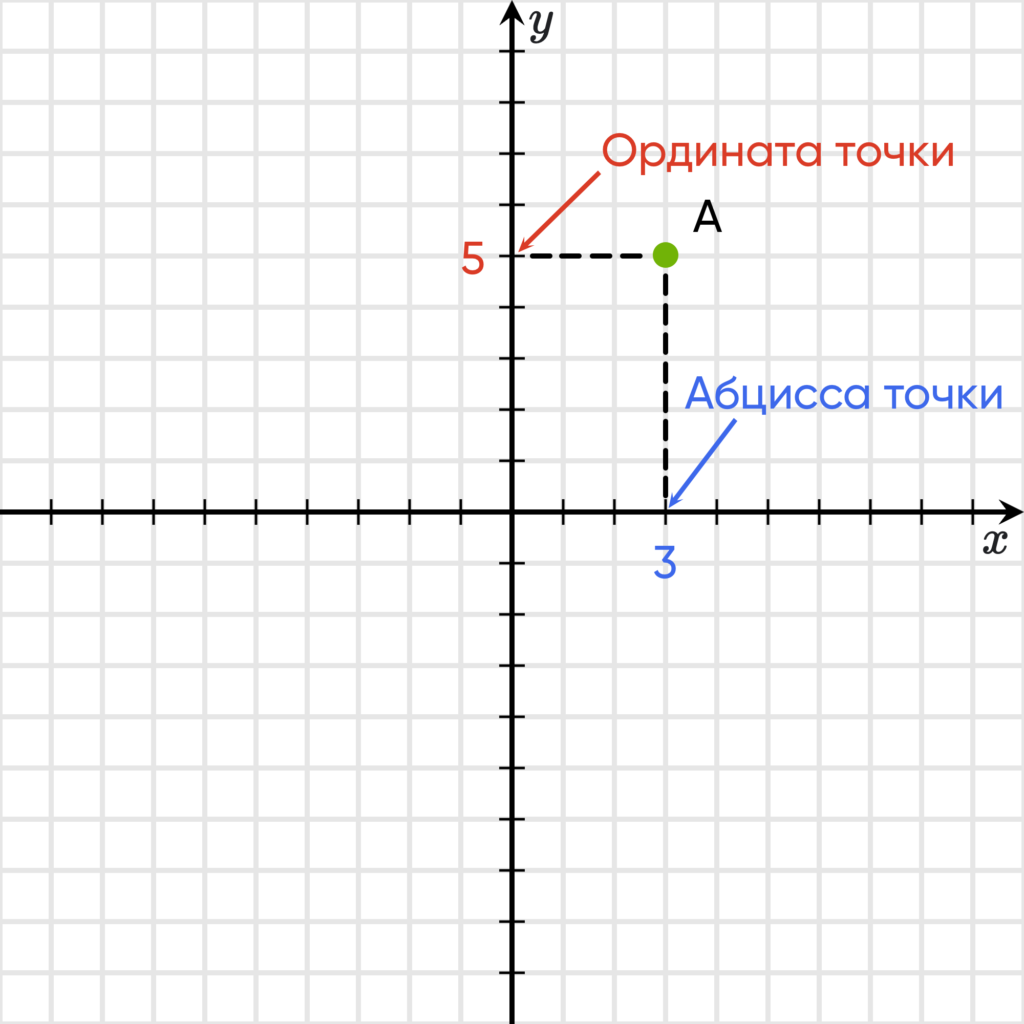
Так на рисунке выше у точки $A$ относительно точки отсчета $О$ координаты будут такими:

• по оси $\color{#3D68EB}x$ — $\color{#3D68EB}3$
• по оси $\color{#eb3d3d}y$ — $\color{#eb3d3d}5$

Координата точки $A$ по оси $Ох$, называется абсциссой точки $А$, координата по оси $у$, называется ординатой точки $А$. 

Принято записывать на первом месте абсциссу, и ординату – на втором месте.

Координата точки $А$ в нашем случае запишется следующим образом: $A(3;5)$

Начало отсчета точка $О$ имеет координаты $(0,0)$

Таким образом, координаты – это числовые значения, с помощью которых выясняется местоположение точки на плоскости.

В прямоугольной системе координат значения координат любой точки можно найти, проведя от нее перпендикулярные пунктирные линии к каждой из осей.

И, наоборот, чтобы найти точку на плоскости с определенными координатами, от каждой из осей $Ох$ и $Оу$ необходимо провести перпендикуляры по заданным координатам. Искомая точка будет находиться в месте пересечения этих перпендикулярных линий.

Особые случаи

1. Если абсцисса (координата $х$) точки равна $0$, то она лежит на оси $Оу$. И, наоборот, если точка лежит на оси $Оу$, то величина ее абсциссы равна $0$. Все точки, лежащие на оси $Оу$, имеют абсциссу $0$

2. Аналогично, если ордината точки равна $0$, то она лежит на оси $Ох$. Все точки, лежащие на оси $Ох$, имеют ординату $0$

3. Если провести прямую линию, перпендикулярную оси абсцисс (или параллельную оси ординат), то все точки этой прямой будут иметь одинаковую абсциссу.

4. Также и с прямой линией, перпендикулярной оси ординат (или параллельной оси $Ох$): все точки на ней будут иметь одинаковые ординаты, то есть координаты по оси $Оу$.