Способы задания функций. График функции
Определить правило, по которому зависимая величина будет меняться, значит задать функцию. Вариантов задания функции несколько:
- Словесно, например: «игрек равен двум х». Запись будет выглядеть так: $у = 2\times x$
- Аналитический способ, то есть сразу с помощью записи формулы, например: $f(x) = x-3$
- Графический способ
- Табличный способ
Графический способ
Графический способ подразумевает чертеж на прямоугольной координатной плоскости, например:

Линия, изображенная на рисунке, называется графиком функции.
Определение:
Линия может быть разной: прямой или кривой.
Функция (и ее график) может быть:
- возрастающей (линия идет вверх, как на рисунке выше), если вторая зависимая величина увеличивается вместе с первой;
- убывающей (линия идет вниз), если вторая величина уменьшается при увеличении первой, например:
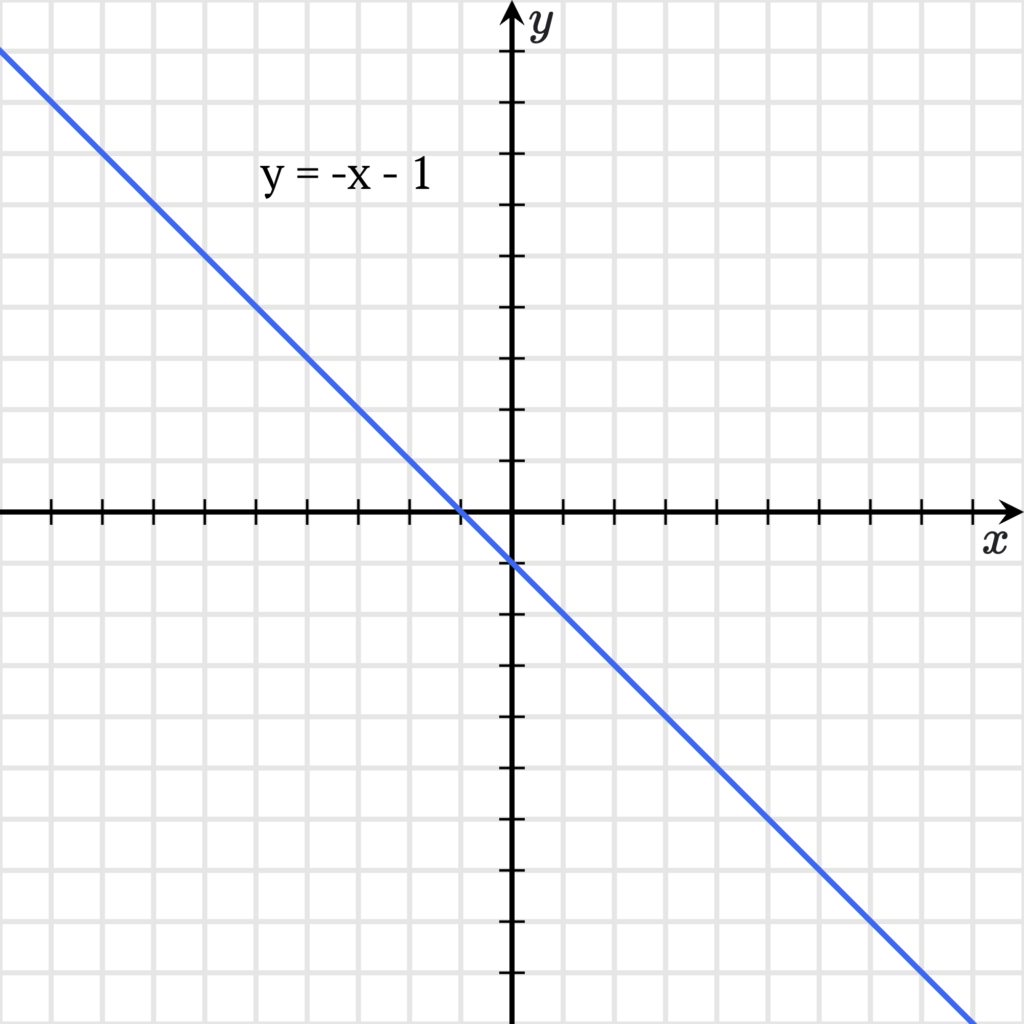
Функция (и ее график) может быть убывающей или возрастающей как на всей области определения, так и на определенном промежутке:
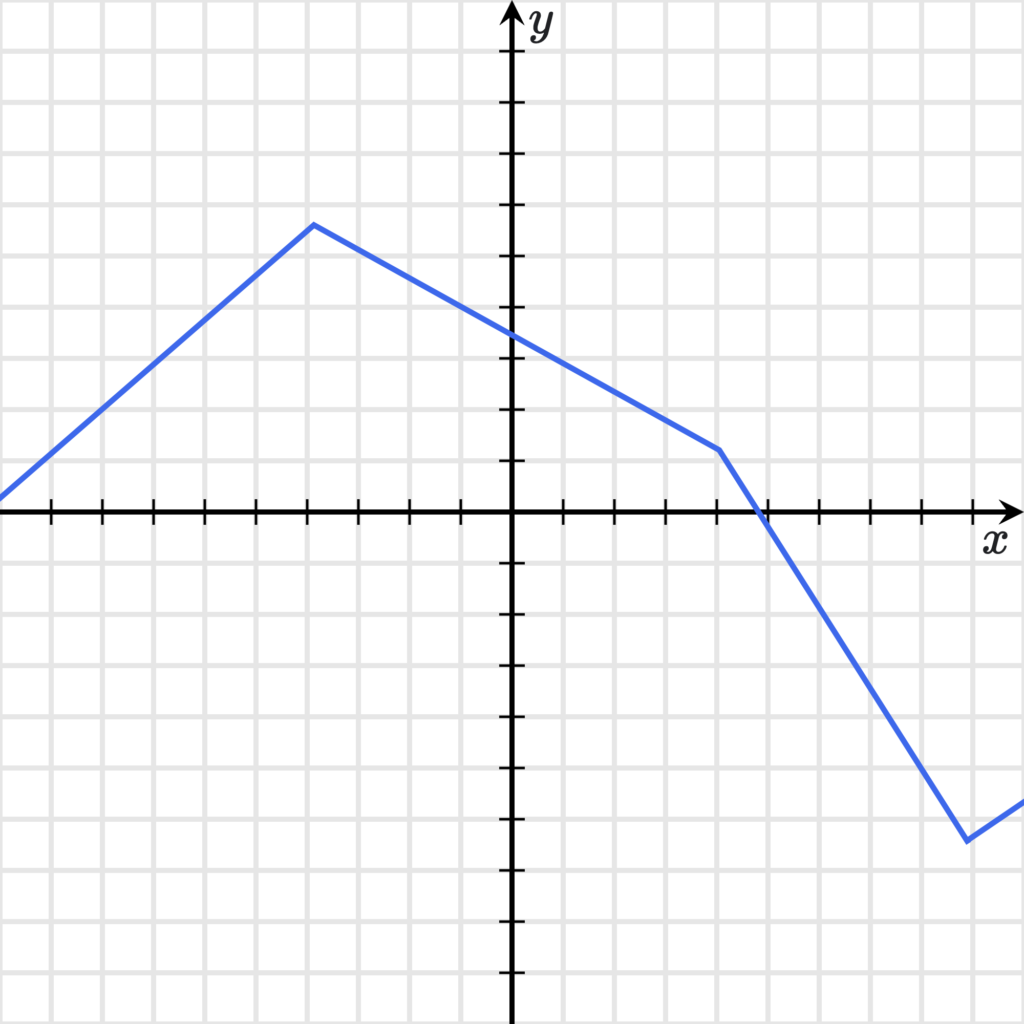
Графический способ не дает возможности предельно точного определения численных значений $x$ и $у$, но он наглядно показывает поведение функции (убывает или возрастает, максимум, минимум, непрерывность и т. д.) и является важным способом ее исследования.
Подробный урок о том, как строить график линейной функции.
Табличный способ
Часто используется табличный (то есть в виде таблицы) способ задания функции. В таблице для каждого значения аргумента $x$ указывается соответствующее ему конкретное значение функции $y$, например:
| $x$ | $1$ | $2$ | $3$ | $5$ |
| $y$ | $10$ | $20$ | $30$ | $50$ |
Каждое значение аргумента и функции нумеруется. В данном случае в таблице значению $x_1$, равному $1$, соответствует единственное значение $у_1$, равное $10$. Значению $x_2$, равному $2$, соответствует $у_2$, равное $20$ и т. д.
Не трудно догадаться, что в таблице выше отражена зависимость
$y = 10x$.
Ее можно продолжить для любых значений $x$, так при
$x_{100} = 100$
$y_{100}$ будет равен $1000$.
Табличный способ позволяет быстро найти конкретные значения $x$ и $у$.
Заполним таблицу для функции
Попробуем заполнить таблицу функции $у=3x+2$, для значений $x$, равных $1$, $3$, $4$, $8$.
Подставим в формулу $у=3x+2$ значения $x_1$, $x_2$, $x_3$, $x_4$.
Получим:
$у_1 = 3\times 1 + 2 = 5$
$у_2 = 3\times 3 + 2 = 11$
$у_3 = 3\times 4 + 2 = 14$
$у_4 = 3\times 8 + 2 = 26$
Заполним таблицу:
| $x$ | $1$ | $3$ | $4$ | $8$ |
| $у$ | $5$ | $11$ | $14$ | $26$ |
Оценить урок
Что можно улучшить?
Войдите, чтобы оценивать уроки
Что нужно исправить?
Отзыв отправлен. Спасибо, что помогаете нам стать лучше!
Для отправки комментария вам необходимо авторизоваться.
