Приближение и округление десятичных дробей
В повседневной жизни мы часто сталкиваемся с необходимостью округлять числа. Например, когда мы говорим о температуре воздуха, то обычно округляем ее до целых чисел (например, $23 °C$ вместо $23,4 °C$). Округленное значение может быть менее точным, но оно легче для понимания и использования.
Вы уже знаете о десятичных дробях и их свойствах. Сегодня мы рассмотрим, что такое округление и приближение десятичной дроби, а также поговорим о том, когда такая дробь может стать бесконечной.
Округление десятичных дробей
Округление любых чисел помогает сделать их более понятными и легкими для восприятия. В обычной жизни часто бывает не важна абсолютная точность. Например, почти всегда вместо цены $199$ рублей вы скажете — $200$ рублей.

Также округление часто используется в точных науках, например, в физике и экономике. Ученые выполняют сложные расчеты, где некоторые значения удобно взять в виде приблизительного числа, которое не повлияет на результат. В математике такое значение мы называем приближенным.
Округление десятичной дроби — это процесс нахождения наиболее близкого по значению к ней числа, где одна или несколько последних ее цифр заменяются нулями.
Например, если нам нужно найти площадь круга, чтобы упростить вычисления, мы можем использовать приближенное значение числа $\pi = 3,14$ вместо его точного значения $3,141592…$.
Точность округления десятичных дробей может быть разной: в какой-то задаче вам достаточно округлить до десятых, в другой — до тысячных. Это условие показывает, до какого разряда после запятой требуется сделать округление.
Правила округления
Для того чтобы округлить десятичную дробь, нужно придерживаться определенного алгоритма действий.
Шаг 1
Определяем разряд, до которого происходит округление.
Округление производится до заданного разряда (целых, десятых, сотых и т. д.). При округлении числа мы не меняем его значение, а лишь упрощаем запись.
Вспомним названия разрядов после запятой в записи десятичной дроби:
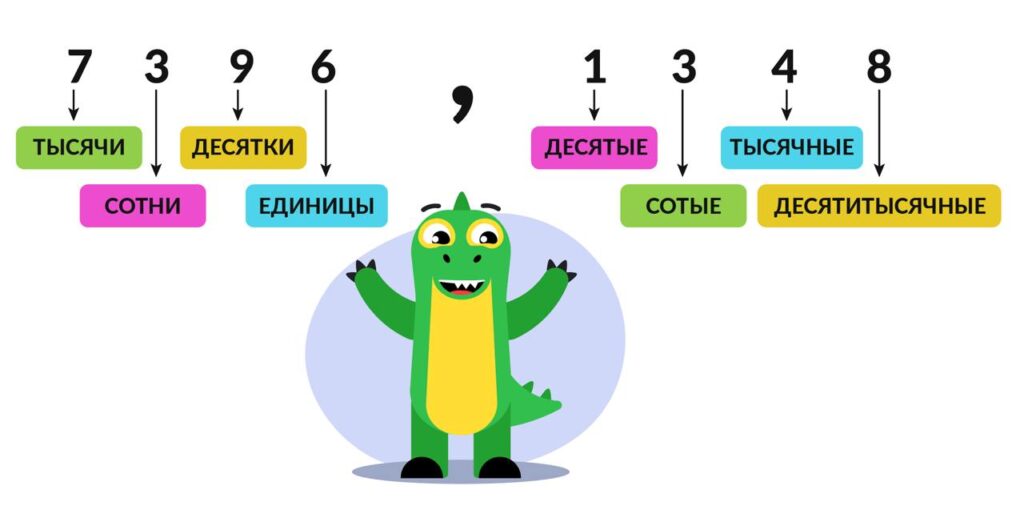
Шаг 2
Смотрим на цифру справа от выделенного разряда: если это $0, 1, 2, 3, 4$, то цифра разряда, до которого округляем, остается без изменений.
Округлим число $6,6539$ до сотых:
- Подчеркнем цифру $5$ и отбросим цифры $3$ и $9$, которые следуют за разрядом сотых.
- За подчеркнутой цифрой $5$ стоит цифра $3$, поэтому цифру $5$ оставляем без изменений.
- Получаем $6,65$.
Шаг 3
Смотрим на цифру справа от выделенного разряда: если она больше или равна $5$, то цифра разряда, до которого округляем, увеличивается на единицу.
Округлим число $5,876$ до сотых:
- Подчеркнем цифру $7$ и отбросим цифру $6$, которая следуют за разрядом сотых.
- За подчеркнутой цифрой $7$ стоит цифра $6$, которая $>5$, поэтому цифру $7$ увеличиваем на $1$.
- Получаем $5,88$.
Шаг 4
Записываем приближенное значение, используя знак $\approx$. Знак читается: «Приблизительно равно».
$6,6539\approx 6,65$ при округлении до сотых.
$5,876\approx 5,88$ при округлении до сотых.
Практика: округление
№1. Приближение в измерениях
Бегун пробежал дистанцию $9,832$ км. В отчете соревнований нужно записать результат с точностью до десятых.
Какое значение судья укажет в отчете?
Показать решение и ответ
Скрыть
Обратим внимание на разряд сотых — $3$. Так как $3 < 5$, то оставляем десятые без изменений.
Ответ: $9,8$ км.
№2. Округление и приближение в задачах с деньгами
В магазине Маша купила шоколадный батончик за $52,79$ рубля. Она платит наличными и хочет заранее подсчитать, сколько у нее останется сдачи, если округлить сумму до ближайшего рубля.
Какую сумму она заплатит, если округлить стоимость до целых рублей?
Показать решение и ответ
Скрыть
Обратим внимание на разряд десятых — $7$. Так как $7 > 5$, то увеличиваем целую часть на $1$.
Ответ: $53$ рубля.
Конечные и бесконечные периодические дроби
Ранее мы всегда работали с десятичными дробями, в записи которых после запятой стоит конечное число цифр. Эти дроби называются конечными десятичными дробями.
Некоторые обыкновенные дроби нельзя записать в виде конечной десятичной дроби, потому что их знаки после запятой повторяются бесконечно. Такое деление можно продолжать бесконечно:
$\frac{1}{3} = 0,33333…$ (бесконечно много троек)
$\frac{2}{11} = 0,181818…$ (повторяется $1$ и $8$)
Периодическая дробь — это десятичная дробь, у которой цифры после запятой повторяются бесконечно.
Как записывать периодические дроби? Допустим, при делении обыкновенной дроби вы получили бесконечную периодическую дробь $0,424242…$. Выделяем повторяющийся фрагмент и записываем дробь как $0,(42)$.
Повторяющуюся часть называют периодом и записывают ее в скобках. Такая запись читается как «ноль целых и сорок два в периоде».
Как определить, какой будет дробь при делении конечной или бесконечной?
Скрыть
Чтобы определить, будет ли обыкновенная дробь $\frac{a}{b}$ периодической при делении, нужно обратить внимание на знаменатель $b$ после сокращения дроби.
- Если знаменатель после сокращения содержит только множители $2$ и/или $5$, то дробь превращается в конечную десятичную.
- Если в знаменателе есть другие числа (кроме $2$ и $5$), то дробь будет бесконечной периодической.
Математический вывод
При делении одного натурального числа на другое можно получить один из трех результатов: натуральное число, конечную десятичную дробь и бесконечную периодическую десятичную дробь.
Практика: конечные и бесконечные дроби
№1. Определите, является дробь конечной или бесконечной
Преобразуйте обычную дробь $\frac{3}{8}$ в десятичную.
Показать решение и ответ
Скрыть
Разложим $8$ на простые множители: $8 = 2 × 2 × 2$ (только двойки).
Значит, $\frac{3}{8} = 0,375$ это конечная дробь.
№2. Определите, является дробь конечной или бесконечной
Преобразуйте обыкновенную дробь $\frac{7}{12}$ в десятичную.
Показать решение и ответ
Скрыть
$12 = 2×2 × 3$. В знаменателе есть $3$.
Значит, $\frac{7}{12} = 0,58(3)$ — бесконечная периодическая дробь.
№3. Определите, является дробь конечной или бесконечной
Преобразуйте обыкновенную дробь $\frac{5}{11}$ в десятичную.
Показать решение и ответ
Скрыть
Знаменатель $11$ — простое число, не делится на $2$ или $5$.
Значит, $\frac{5}{11} = 0,(45)$ — это бесконечная периодическая дробь.
Перевод периодической десятичной дроби в обыкновенную
Чтобы понять, как выполнить обратное преобразование бесконечной десятичной дроби в обыкновенную, рассмотрим алгоритм на примере числа $0,333…$ или $0,(3)$:
- Возьмем за $x$ наше число: $x=0,333…$
- Умножим на $10$, чтобы период сместился: $10x=3,333…$
- Вычтем первое уравнение из второго:
$10x−x=3,333…−0,333… $
$9x=3$ - Разделим обе части уравнения на $9$:
$x= \frac{3}{9} = \frac{1}{3}$.
Часто задаваемые вопросы
Если после нужного знака разряда стоят цифры $5, 6, 7, 8, 9$, то предыдущую цифру увеличиваем на $1$.
Если цифры $0, 1, 2, 3, 4$, то просто убираем ее.
При делении нужно обратить внимание на знаменатель после сокращения дроби. Если в знаменателе есть другие числа, кроме $2$ и $5$, то дробь будет бесконечной периодической.
Натуральное число, конечная или бесконечная десятичная дробь.

Хотите оставить комментарий?
Войти