Измерение физических величин. СИ
Спектр объектов и явлений, изучаемых в физике, огромен. От невероятной скорости электромагнитной волны до возраста Земли и от крошечных размеров частиц до площади наблюдаемой вселенной. От силы, создаваемой прыгающей блохой, до силы притяжения между Землей и Луной.
Мы определяем физическую величину либо путем измерения с помощью соответствующих приборов, либо путем расчета на основе других измерений. Например, мы определяем расстояние, полагаясь на то, что оно рассчитывается как скорость, умноженная на время в пути.
Однако все известные физические величины выражаются в единицах, которые являются стандартизованными значениями. Например, длина забега, которая тоже является физической величиной, может быть выражена в метрах (для спринтеров) или в километрах (для бегунов на длинные дистанции). Без стандартизированных единиц ученым было бы чрезвычайно сложно вычислить и сравнить измеренные значения.
Что значит измерить какую-либо величину?
Измерить какую либо величину — это значит сравнить ее с однородной величиной, принятой за единицу.
Система единиц измерения
Во всем мире используются такая система единиц измерения как «единицы СИ» (сокращение от французского Le Système International d’Unités, также известное как метрическая система). Некоторые физические величины и их единицы измерения представлены в таблице 1.
| Основные величины | Символ | Единица СИ |
|---|---|---|
| Масса | $m$ | килограмм ($кг$) |
| Время | $t$ | секунда ($с$) |
| Температура | $T$ | кельвин ($К$) |
| Длина | $l, S$ | метр ($м$) |
| Скорость | $\upsilon$ | метр в секунду ($\frac{м}{c}$) |
Каковы единицы длины, времени, массы в СИ?
В этой системе основной единицей длины является метр (м), единицей времени — секунда (с), единицей массы — килограмм (кг). Но так было не всегда!
Существует также такая система единиц измерения как имперская система или английские единицы измерения. Эта система исторически использовались в странах, когда-то находившихся под управлением Британской империей. Сегодня Соединенные Штаты — единственная страна, в которой до сих пор широко используется имперская система.
Часто, когда мы применяем систему единиц СИ, нам может понадобиться выразить единицы, которые больше принятых единиц в 10, 100, 1000 раз (таблица 2). Здесь все просто — к наименованиям единиц СИ нужно добавить соответствующую приставку на греческом языке:
если эта единица больше СИ в 10 раз — к названию добавляется приставка «дека», в 100 раз — «гекто», в 1000 раз — «кило» и т.д. Такие приставки называю кратными.
Если же нужно выразить единицы, которые меньше принятых в 10, 100, 1000 раз, то к названиям единиц добавляются приставки на латинском языке: «деци», «санти», «милли» и т.д. Такие приставки называют дольными.
| Обозначение | Название | Множитель |
| г | гекто | $100$ (или $10^2$) |
| к | кило | $1000$ (или $10^3$) |
| М | мега | $1 \space 000 \space 000$ (или $10^6$) |
| д | деци | $0.1$ (или $10^{-1}$) |
| с | санти | $0.01$ (или $10^{-2}$) |
| м | милли | $0.001$ (или $10^{-3}$) |
Пример:
Пачка макарон весит 300 грамм (г). Выразите ее вес в килограммах (кг).
Для того чтобы решить эту задачу, нам нужно вспомнить, что в одном килограмме — 1000 грамм. Следовательно, нам всего лишь остается разделить 300 грамм на 1000. Получается, что в килограммах, пачка макарон будет весить 0,3 кг.
Единицы измерения в ходе истории
В древние времена человек использовал части своего тела в качестве инструментов измерения, такие как рука, ладонь и ступня. А для измерения времени использовали природные явления, такие как восход, закат и фазы Луны.
Так, в Древней Руси мерой длины мог быть сам человек (рисунок 1). Например, косая сажень — расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь, или четверть, — расстояние между концами расставленных большого и указательного пальцев руки.
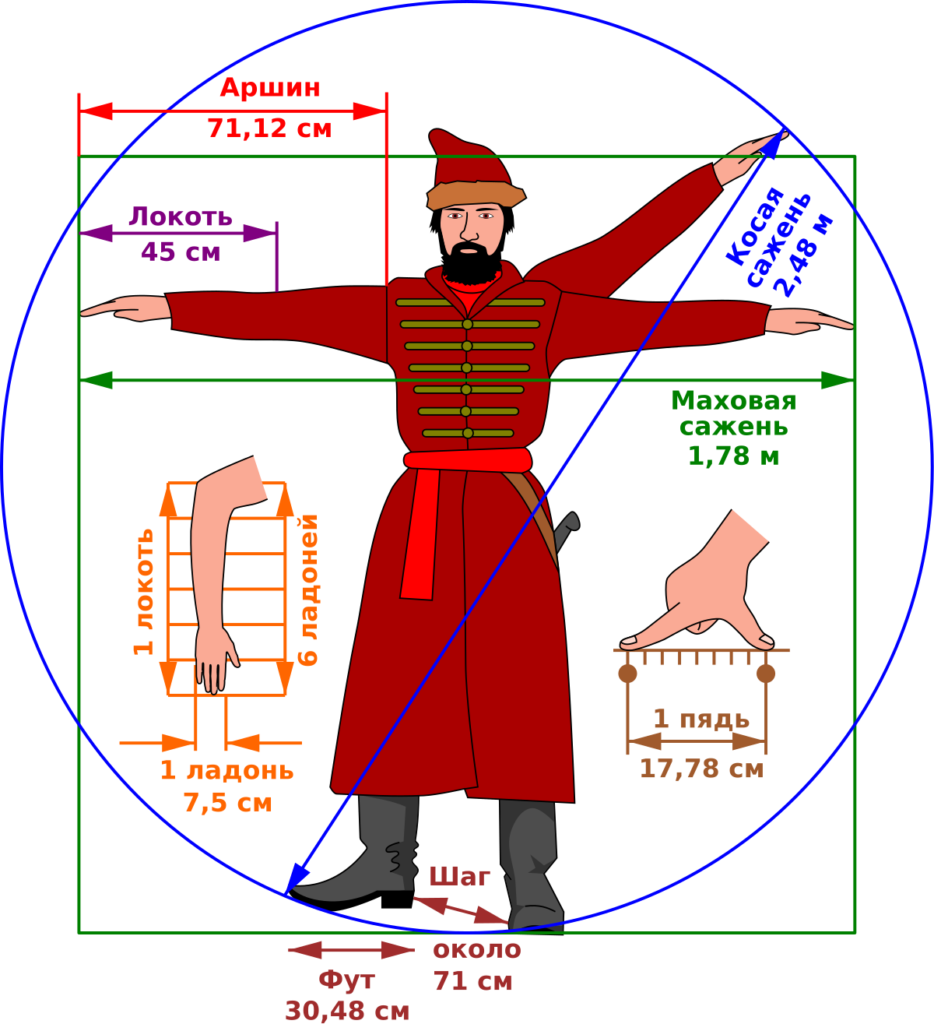
Измерительные инструменты со временем совершенствовались, они были необходимы человеку в точном описании явлений и изучении законов физики.
Используемый измерительный инструмент зависит от измеряемой физической величины. Для измерения длины существуют такие инструменты, как линейка, штангенциркуль и микрометр.
Для получений различных параметров электрического тока — амперметр, вольтметр, омметр. Для вычисления времени, мы прибегнем к использованию таймеров и секундомеров.
Цена деления
Как правило, все измерительные приборы имеют свою шкалу. Для точности подсчета, на панель прибора нанесено несколько делений, подписанных соответствующими значениями, между которыми, в свою очередь, находится еще несколько делений поменьше, обычно эти промежуточные деления числами не обозначены.
В науке об измерениях, такие деления показывают наименьшее и самое точное значение измеряемой величины, и называются они — цена деления. Как нетрудно догадаться, что чем меньше цена деления, тем точнее измерения.
Например, на наручных часах могут быть только 12 отметок часов текущего времени суток, то есть цена деления этого прибора — один час.
Секундомер, используемый для измерения времени при проведении спортивных состязаний, может иметь цену деления до сотых долей секунды. Все потому, что секундомер более точен при измерении временных интервалов, чем обычные часы, поэтому у него больше «интервалов» в каждый час прошедшего времени.
Цена деления — одна из самых важных характеристик для получения точных показаний такого инструмента, как штангенциркуль, используемого в различных экспериментах.
Как определяется цена деления измерительного прибора?
Для определения цены деления любого измерительного прибора необходимо:
- Определить два ближайших штриха на шкале, возле которых стоят значения величины;
- Вычесть из большего значения меньшее;
- Полученное число разделить на число делений, находящихся между ними.
Давайте для наглядности найдем цену деления термометра, изображенного на рисунке 2.
Возьмем два соседних штриха, около которых стоят цифры (значения температуры). Пусть это будут штрихи с обозначениями $10 \degree C$ и $20 \degree C$. Между этими штрихами 10 делений.
Определим цену деления:
$\frac{20 \degree C — 10 \degree C}{10} = 1 \degree C$.
Получается, что термометр показывает $26 \degree C$.
Упражнения
Упражнение №1
Определите цену деления секундомера (рисунок 3).
Показать решение и ответ
Скрыть
Решение:
Возьмем два соседних штриха, которые отмечены цифрами: 5 с и 10 с. Между ними находится 10 делений. Найдем цену деления этого секундомера:
$\frac{10 \space с — 5 \space с}{10} = 0.5 \space с$.
Ответ: цена деления секундомера равна $0.5 \space с$.
Упражнение №2
По рисунку 4 определите цену деления амперметра (рисунок 4, а) и вольтметра (рисунок 4, б).
Показать решение и ответ
Скрыть
Решение:
Для амперметра (рисунок 4, а):
возьмем соседние значения 0 А и 0.5 А. Между ними находится 10 делений.
Найдем цену деления прибора:
$\frac{0.5 \space А -0 \space А}{10} = 0.05 \space А$.
Для вольтметра (рисунок 4, б):
возьмем соседние значения 0 В и 1 В. Между ними находится 5 делений.
Найдем цену деления прибора:
$\frac{1 \space В — 0 \space В}{5} = 0.2 \space В$.
Ответ: цена деления амперметра равна $0.5 \space А$, а вольтметра — $0.2 \space В$.
Задания
Задание №1
Используя интернет, найдите прибор для измерения артериального давления — тонометр механический. Определите цену деления шкалы. В каких единицах измеряют артериальное давление?
Механический тонометр изображен на рисунке 5.
Показать решение и ответ
Скрыть
Решение:
Артериальное давление измеряют в мм рт. ст. (миллиметрах ртутного столба). Возьмем два соседних деления, обозначенных цифрами: 20 мм рт. ст. и 40 мм рт. ст. Между ними находится 10 делений. Определим цену деления прибора:
$\frac{40 \space мм \space рт. \space ст. — 20 \space мм \space рт. \space ст.}{10} = 2 \space мм \space рт. \space ст.$
Ответ: $2 \space мм \space рт. \space ст.$
Задание №2
Найдите старинные меры объема, используемые в Древней Руси.
Производные от длины меры объемы в Древней Руси приведены в таблице 3.
| Древнерусская мера объема | Современные единицы измерения |
| 1 куб. сажень | $9.7127 \space м^3$ |
| 1 куб. аршин | $359.7288 \space дм^3$ |
| 1 куб. фут | $28.3168 \space дм^3$ |
| 1 куб. вершок | $87.8244 \space см^3$ |
| 1 куб. линия | $16.3871 \space мм^3$ |
Также были распространены и другие меры объема. В таблице 4 представлены меры объема, которые использовали для сыпучих тел (например, крупы).
| Мера объема | Литры |
| Цебр | 5457,5872 — 6297,216 |
| Кадка | 839,69 |
| Четверть | 209,9072 |
| Осьмина | 104,95 |
| Четверик | 26,2387 |
| Гарнец | 3,2798 |
| Стакан | 0,273 |
Для жидкостей использовали другие меры объема. Они представлены в таблице 5.
| Мера объема | Литры |
| Шкалик | 0,0615 |
| Чарка | 0,123 |
| Водочная бутылка | 0,614962 |
| Винная бутылка | 0,7687 |
| Штоф | 1,2299 |
| Четверть | 3,0748 |
| Ведро | 491,976 |
| Бочка | 491,976 |
Задание №3
Выразите свой вес в пудах, а рост в аршинах.
Возьмем для примера следующие параметры: рост равен $145 \space см$, а вес — $42 \space кг$.
1 пуд приблизительно равен $16.3807 \space кг$, а 1 аршин — $71.12 \space см$. Переведем в эти единицы рост и вес.
Рост:
$\frac{145 \space см}{71.12} \approx 2 \space аршина$.
Вес:
$\frac{42 \space кг}{16.3807 \space кг} \approx 2.6 \space пуда$.
Задание №4
Запишите 2-3 пословицы, поговорки или образных выражения, в которых упоминаются старинные меры длины, массы, объема и т.п.
Примеры:
- Семь пядей во лбу
- Косая сажень в плечах
- Зернышко пуд бережет
- Борода с аршин, а сам с кувшин
- Человека узнаешь, когда с ним пуд соли ложкой расхлебаешь
- От слова до дела — целая верста
- Каждый купец на свой аршин мерит
- От горшка два вершка
- Свой золотник чужого пуда дороже
Оценить урок
Что можно улучшить?
Войдите, чтобы оценивать уроки
Что нужно исправить?
Отзыв отправлен. Спасибо, что помогаете нам стать лучше!
Для отправки комментария вам необходимо авторизоваться.

Класс!